Das hört sich natürlich sehr kompliziert an (wenn du es überhaupt
lesen konntest :) aber in Wirklichkeit ist das alles furchtbar einfach.
In den Worten der heutigen Mathematik ausgedrückt wurde in der obenstehenden
Aufgabe ein Strahlensatzproblem gelöst. Das bedeutet, wir haben
es mit einer Aufgabe zu tun, in der mehrere Strahlen mit dem gleichen Anfangspunkt
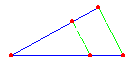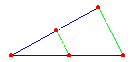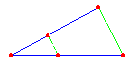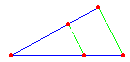
z von mehreren Parallelen geschnitten werden. Das heisst dann Strahlensatzfigur
(siehe Bild unten)!
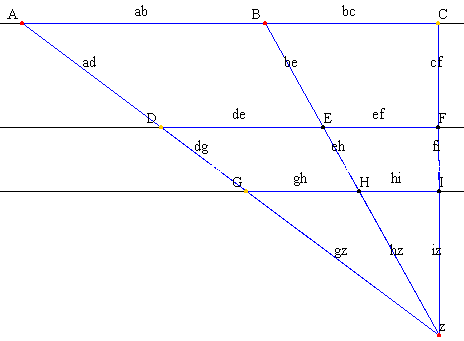Wie im Bild deutlich zu sehen ist (blau gekennzeichnet) entstehen dabei
Abschnitte auf den Strahlen sowie Abschnitte auf den Parallelen. Der Strahlensatz
besagt nun, dass man zwischen den einzelnen Abschnitten Verhältnisse
herstellen kann. Wie das genau funktioniert wird etwas später erklärt.
Jetzt kannst du dir erst noch mal zwei berühmte Beispiele anschauen,
in denen mit Hilfe des Strahlensatzes zum einen der Erdradius und zum anderen
die Höhe einer Felswand auf der "geheimnisvollen Insel" bestimmt wurden.
1. Beispiel:
Berechnung der Höhe einer Felswand in Jules Vernes Roman
"Die geheimnisvolle Insel"
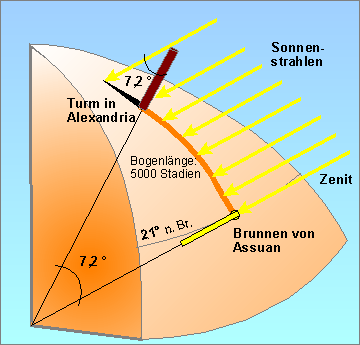
2. Beispiel:
Berechnung des Erdradius durch Eratosthenes!
(ca. 200 v. Chr. )
|
|
[ Weiter zu den Strahlensätzen
]
|
