Die Strahlensätze

Hier sind sie also - die Strahlensätze

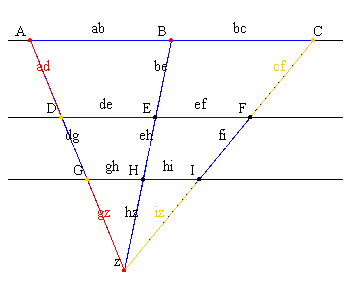
Sicher wirst du schon festgestellt haben, dass immer von "den Strahlensätzen" im Plural die Rede ist. Das hat auch einen Grund: es gibt nämlich zwei Strahlensätze - oder genau genommen zwei Teile des Strahlensatzes! Diese Teile unterscheiden sich aber mehr oder weniger nur durch die Lage der Parallelen - bzw. Strahlenabschnitte. Gehen wir der Reihe nach vor:

Der erste Strahlensatz (oder der Strahlensatz - erster Teil)

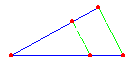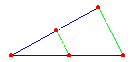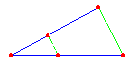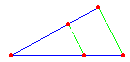
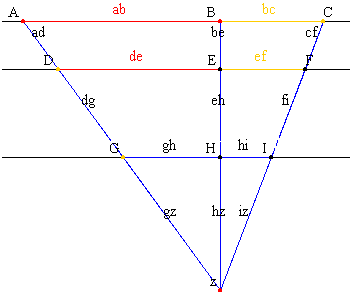
Bei diesem Teil des Strahlensatzes betrachtet man Abschnitte, die alle entweder nur auf den Strahlen (Bild links) oder nur auf den Parallelen liegen (Bild rechts).

[ als Java-Applet ]

[ als Java-Applet ]

1. Strahlensatz
Werden zwei Strahlen mit einem gemeinsamen Anfangspunkt von zwei Parallelen geschnitten, so verhalten sich die Längen von je zwei Streckenabschnitten auf dem einen Strahl wie die Längen der entsprechenden Streckenabschnitte auf dem anderen Strahl. (Bild links)

Das gilt natürlich auch für die Streckenabschnitte auf Parallelen:

Werden zwei Strahlen mit einem gemeinsamen Anfangspunkt von zwei Parallelen geschnitten, so verhalten sich die Längen von je zwei Streckenabschnitten auf der einen Parallelen wie die Längen der entsprechenden Streckenabschnitte auf der anderen Parallelen. (Bild rechts)

Der zweite Strahlensatz (oder der Strahlensatz - zweiter Teil)

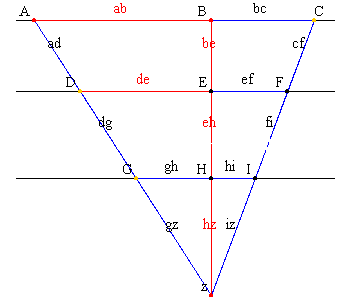
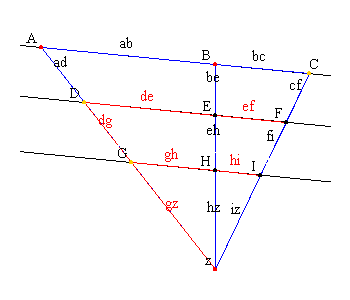
Beim zweiten Teil des Strahlensatzes betrachtet man Abschnitte, die sowohl auf den Strahlen als auch auf den Parallelen liegen (Bild links und Bild rechts).

[ als Java-Applet ]

[ als Java-Applet ]

2. Strahlensatz
Werden zwei Strahlen mit einem gemeinsamen Anfangspunkt von zwei Parallelen geschnitten, so verhalten sich die Längen der Parallelenabschnitte wie die vom Anfangspunkt aus gemessenen Abschnitte auf ein und demselben zugehörigen Strahl.

Übungen
(Fenster mit den Übungen danach einfach wieder schliessen!)

[ Verhältnisse bilden (I) ] [ Verhältnisse bilden (II) ]	In dieser Übung musst du beweisen, dass du Verhältnisgleichungen mit Hilfe der Strahlensätze aufstellen kannst. (I) - mit Hilfestellung (II) - ohne Hilfestellung
[ Gleichungen lösen ]	Hier geht es nur im die Berechnung von Verhältnisgleichungen.
[ Grössen berechnen ]	In dieser Übung musst du zuerst die Verhältnisgleichungen aufstellen und anschliessend lösen.
[ Sachaufgaben lösen ]	Bei diesen Beispielen kannst du zeigen, dass du die Strahlensätze auch auf praktische Problemstellungen übertragen kannst.
[ Strahlensatzfigur bearbeiten ]	Zum Schluss kannst du nun noch ein wenig mit der Strahlensatzfigur herumexperimentieren: -Strahlen oder Parallelen hinzufügen -umbenennen -Animationen ausführen -Konstruktionsbeschreibungen lesen

[ Zurück zur Startseite ]