|
Dynamische Geometrie mit GeoGebra Mit Hilfe von Programmen der dynamischen Geometrie
kann man Konstruktionen, die auf Papier mit Zirkel und Lineal immer nur
statisch sind, dynamisch gestalten. Man kann beispielsweise fertige
Konstruktionen überprüfen, ob sie nur sauber gezeichnet oder aber wirklich
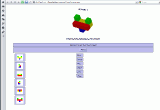
konstruiert worden sind. Dazu kann man freie Punkte (rot
dargestellt) und Gleiter-Punkte (gelb
dargestellt) bewegen. Bleibt die Konstruktion erhalten wurde richtig
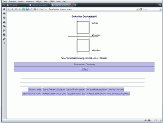
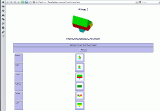
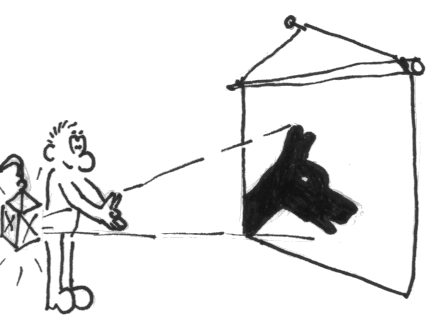
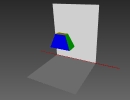
konstruiert - verformt sie sich hingegen sind Fehler aufgetreten! Beispiel einer GeoGebra-3D-Konstruktion: Die Geschwindigkeit für die Wiedergabe der Konstruktion kann eingestellt werden. Um Körper - die ja dreidimensionale Objekte sind - auf einer zweidimensionalen Zeichenebene abbilden zu können müssen wir eine Projektion des Körper realisieren. Das Prinzip gleicht der Schattenprojektion beim Schattenspiel:
Es gibt jedoch wichtige Unterschiede: |
|
|
Schrägbildprojektion 1. Man verwendet parallel verlaufende Projektionsstrahlen (ähnlich wie beim Sonnenlicht) um Verzerrungen zu vermeiden.
|
Zweitafelprojektion 1. Man verwendet parallel verlaufende Projektionsstrahlen (ähnlich wie beim Sonnenlicht) um Verzerrungen zu vermeiden.
|
|
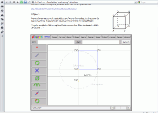
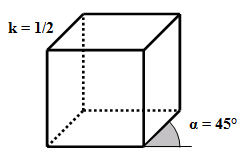
Als Schrägbild bezeichnet man die parallele Projektion eines Körpers auf eine Zeichenebene. Dabei werden Tiefenlinien mit dem Faktor ½ verkürzt und unter einem Winkel von 45° dargestellt (Kavaliersperspektive). Verdeckte Körperkanten werden gestrichelt dargestellt. |
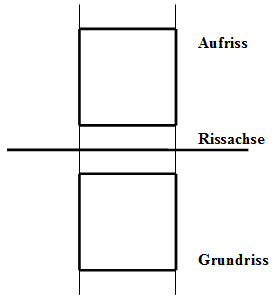
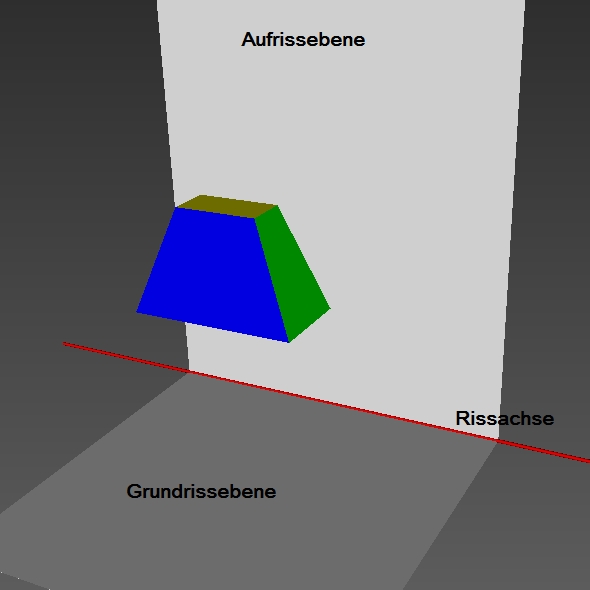
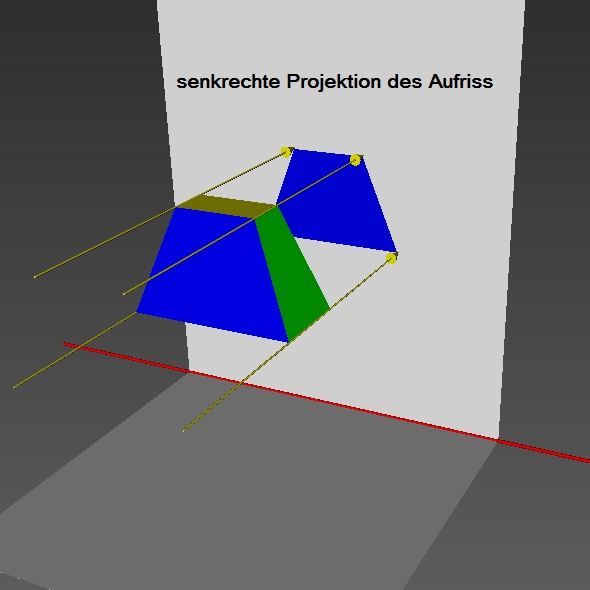
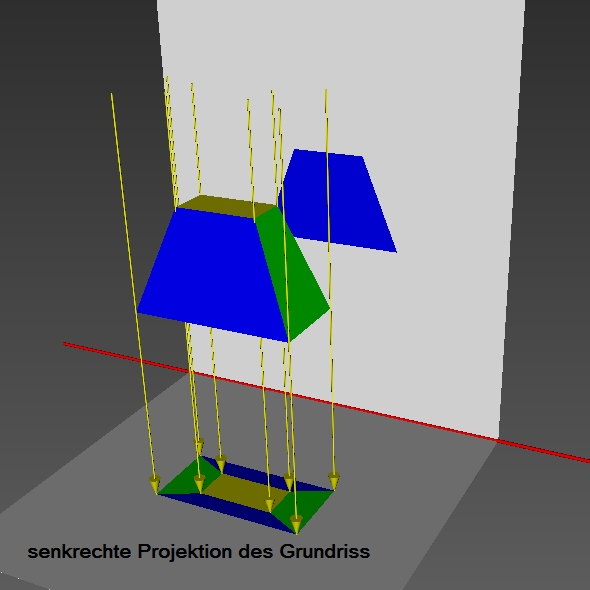
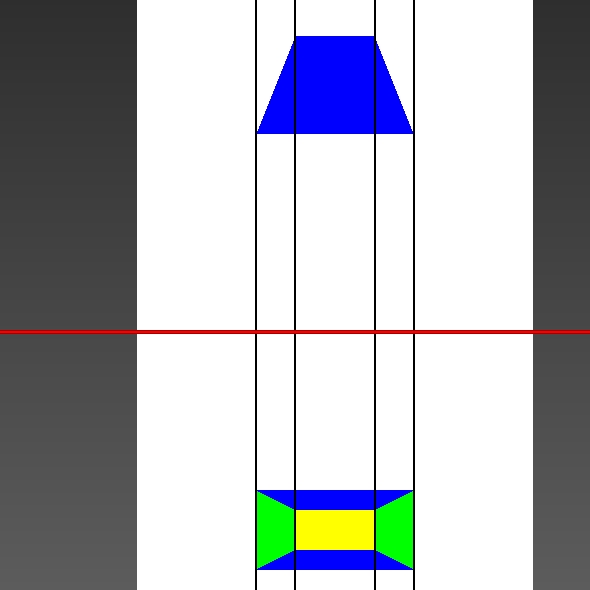
Merke: Als Zweitafelbild bezeichnen wir die senkrechte Parallelprojektion eines Körpers auf zwei Projektionsebenen. Man unterscheidet den Aufriss vom Grundriss. Die beiden Risse werden durch die Rissachse getrennt. |









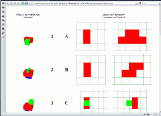
 Jetzt seid ihr dran ...
Jetzt seid ihr dran ...