 |
Alle Aufgaben dieser Seite beziehen sich auf Funktionen
mit den Funktionsgleichungen
Wenn du Hilfe brauchst, verwende den Funktionsgraphen-Plotter
um
[ HILFE ] |
 |
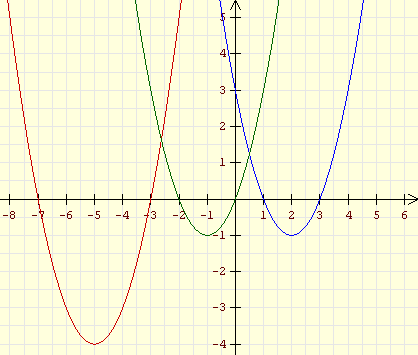
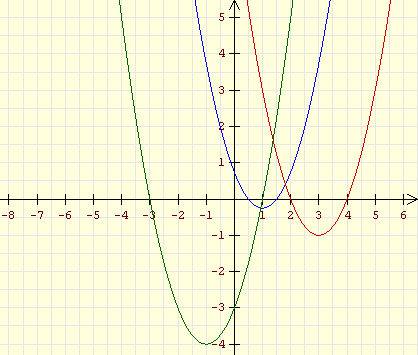
Alle Aufgaben dieser Seite beziehen sich auf Funktionen
mit den Funktionsgleichungen
Wenn du Hilfe brauchst, verwende den Funktionsgraphen-Plotter
um
[ HILFE ] |
|
|
|
 |
|
 |
Zusatz: Interaktive Dateien mit dem GeoGebra-Applet ( 1 mb!! )