In dieser Unterrichtseinheit kommen die Vorzüge von Derive sehr gut zum Tragen! Nachdem man die Unterrichtseinheit bestimmte Ober- und Untersummen zeichnen und berechnen abgeschlossen hat stellt sich nun für den Schüler unweigerlich die Frage: Wie kann man diese Berechnungen für sehr große n (z.B. 100 000 oder 1000 000) durchführen. Hier versagt nun die herkömmliche Mathematik! Aber für Derive ist das überhaupt gar kein Problem...
Wenn man sich die Formeln zur Berechnung der n-ten Ober- und Untersummen hergeleitet hat...

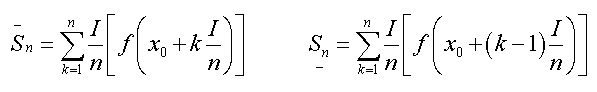
So kann man sehr anschaulich demonstrieren, daß die Grenzwerte von Ober- und Untersumme existieren und übereinstimmen! In diesem Punkt glänzt auch die Darstellung der Formeln auf dem Derive-Dokument: Der Schüler sieht hier, daß Derive genau das macht, was er zuvor im Heft mühevoll berechnet hat.

Das alles erspart es uns aber nicht, daß diese Grenzwerte auch mit Papier und Bleistift berechnet werden müssen! Aber jetzt weiß der Schüler, worauf die Sache hinausläuft...
Und auch das Ersetzten der Folge der Quadratzahlen (Kubikzahlen, Potenzzahlenfolgen mit fast beliebigen Exponenten) ist mit Hilfe von Derive sehr leicht zu begründen - einfach die gesuchte Folge von 1 bis n berechnen lassen - fertig!

Nach einer notwendigen Anzahl handschriftlicher Grenzwertberechnungen der Form
Grenzwertbildung von Ober- und Untersummen ist der Schüler reif zum Bilden der ersten Stammfunktion.

Dazu werden einige einfache Funktionen mittels Grenzwertbildung von Ober- und Untersummen in verschiedenen Intervallen systematisch untersucht und ein Zusammenhang zwischen der Fläche A und dem Funktionswert f(x) hergestellt.
Arbeitsblatt Finden der Stammfunktion. Auch dazu kann man Derive hervorragend einsetzen.

Für die Berechnungen der Ober- und Untersummen verwende ich das Utility OberUnterSumme_ut.mth. Wenn man das OberUnterSumme_ut.mth als Zusatzdatei lädt, dann steht die Funktion Intervall(n,x0,x1) zur Verfügung, welche gleichzeitig die n-te Ober- und Untersumme einer vorher definierten Funktion anzeigt.

Meine Erfahrungen mit den 5° año in unserer Schule waren so positiv, daß ich auch in den nächsten Jahren mit Sicherheit wieder Derive verwenden werde!