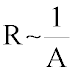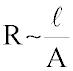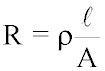Kapitel 8: Das Widerstandsgesetz

Das  Widerstandsgesetz  beschreibt den Zusammenhang zwischen dem elektrischen Widerstand eines Leiters und dem physikalischen Aufbau des Leiters.

Da der Widerstand die Behinderung des el. Stromes kennzeichnet, muss der Aufbau des Leiters offensichtlich etwas mit der Geometrie des Leiters - und somit des Metallgitters - zu tun haben.

Analog zu einem Wasserrohr - welches das hindurchströmende Wasser um so mehr behindert je kleiner der Querschnitt des Rohres ist - kann man vermuten, dass der Querschnitt des Leiters die Behinderung des el. Stromflusses beeinflusst.

Schauen wir uns das in unserer el. Schaltung einmal genauer an:

[ VRML-Animation ( 5 KB, Vollbild, interaktiv ) ]

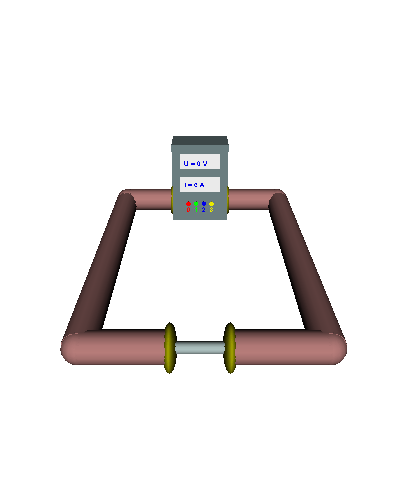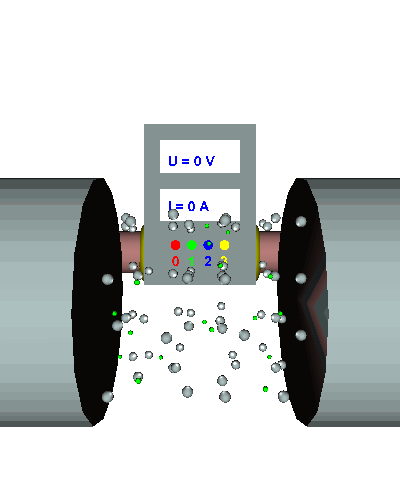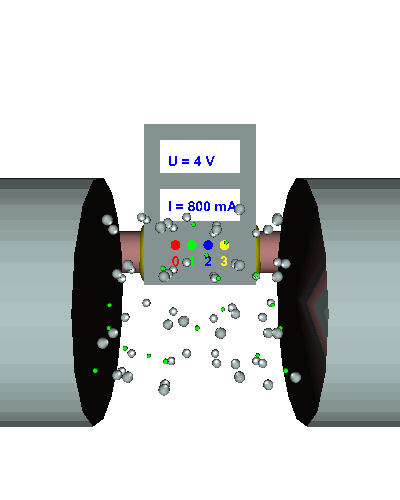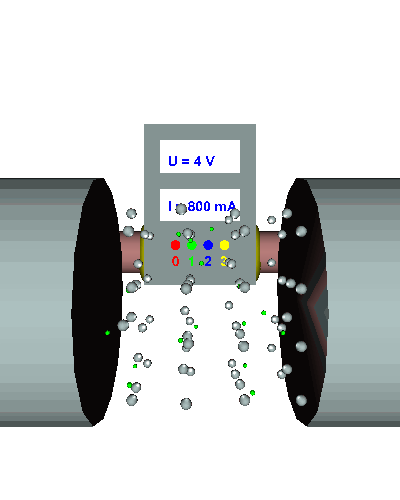
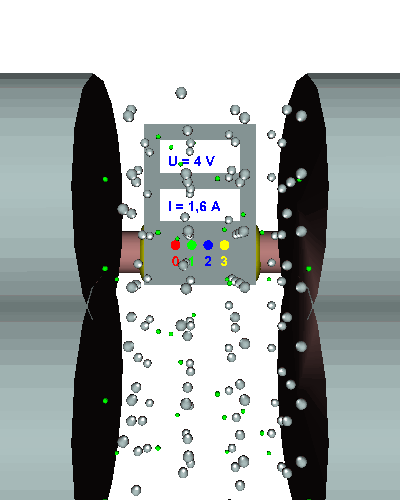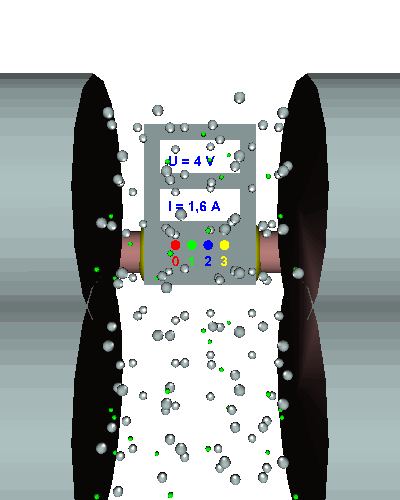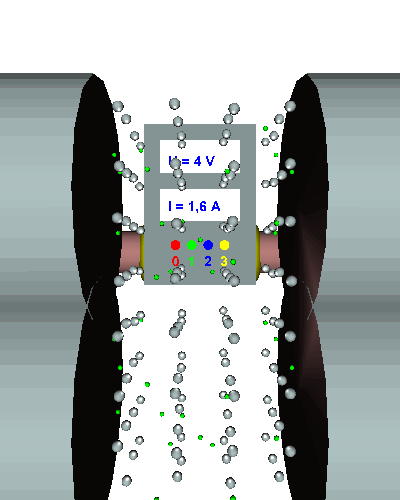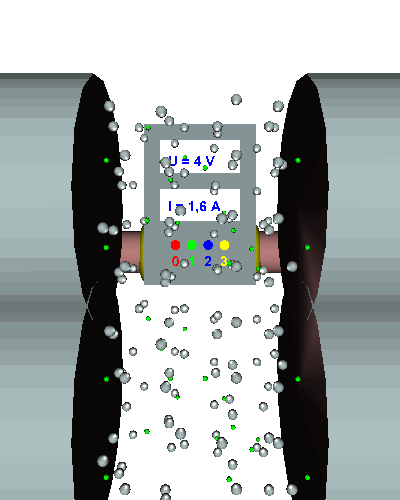
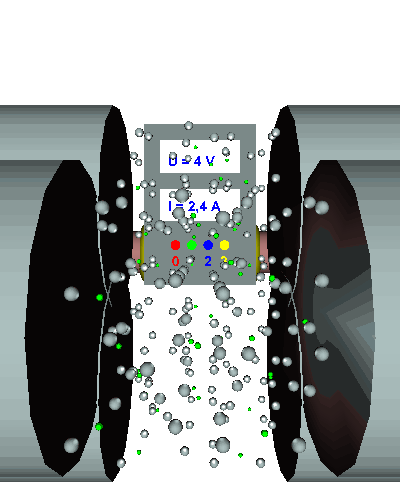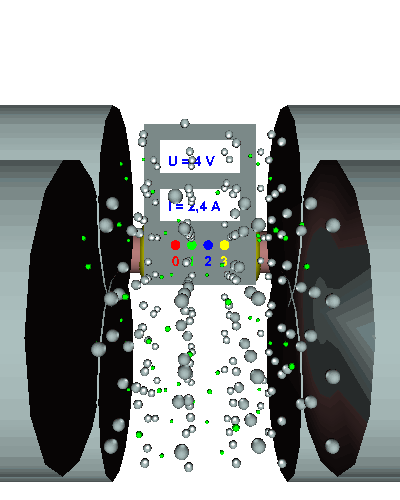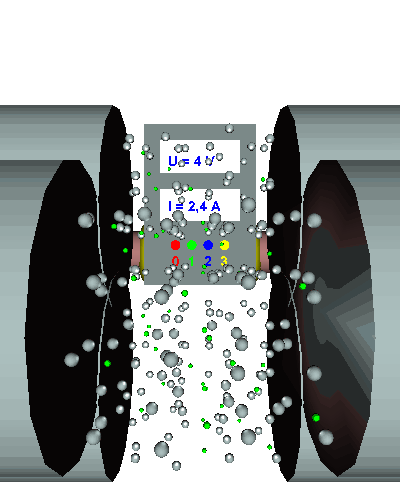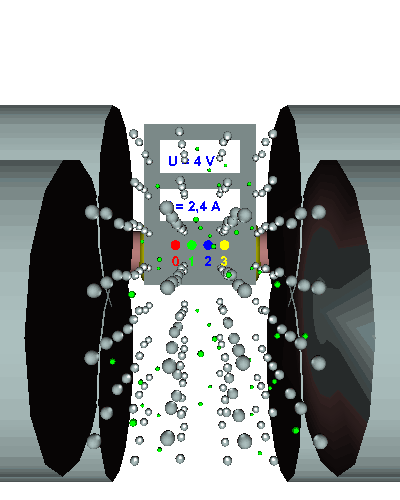
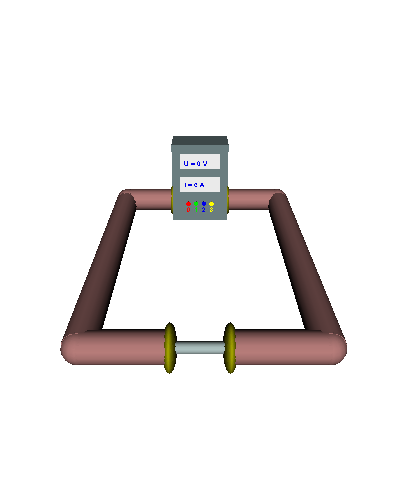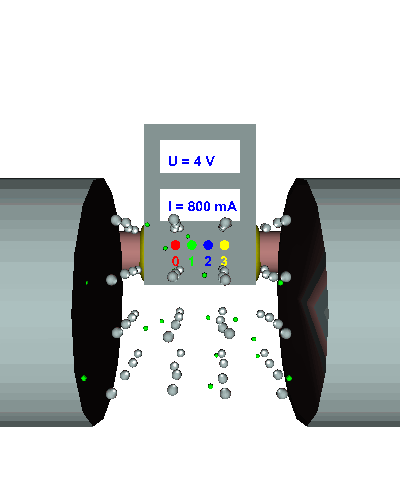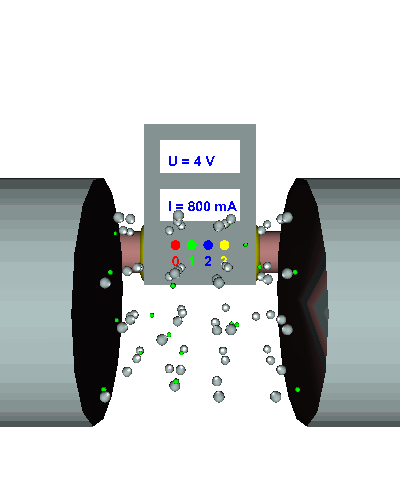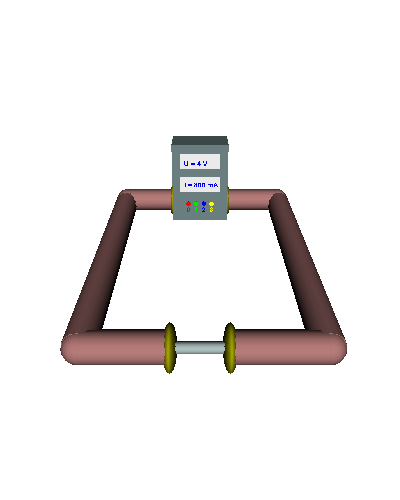
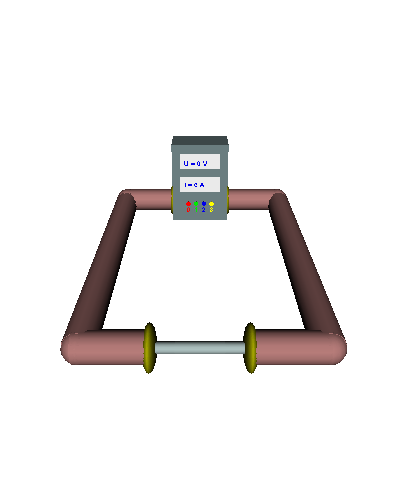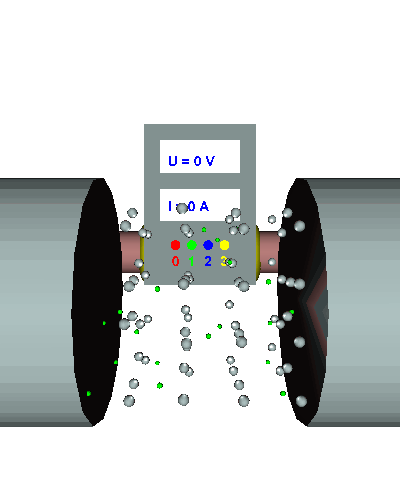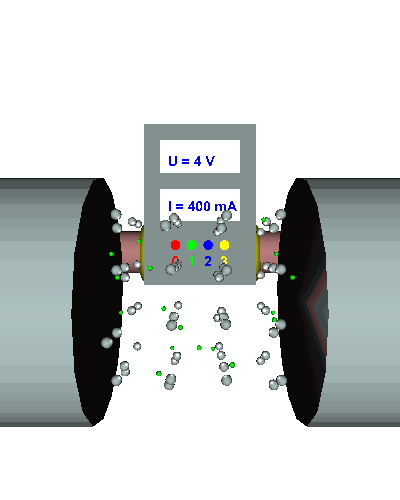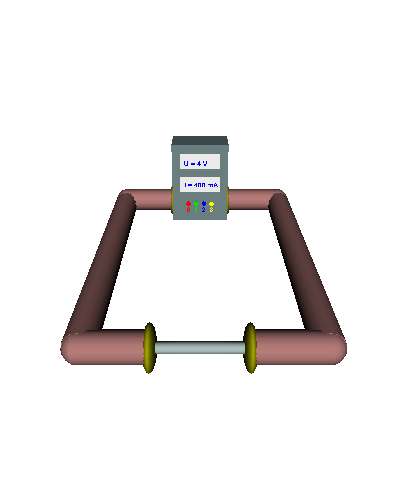
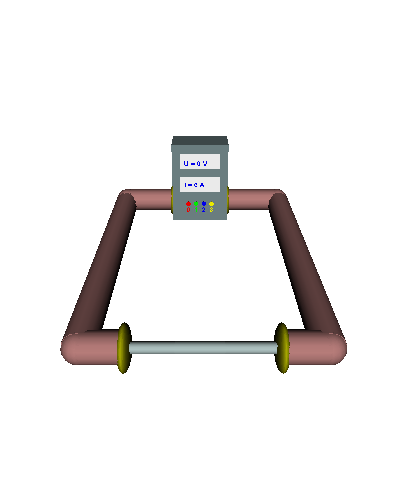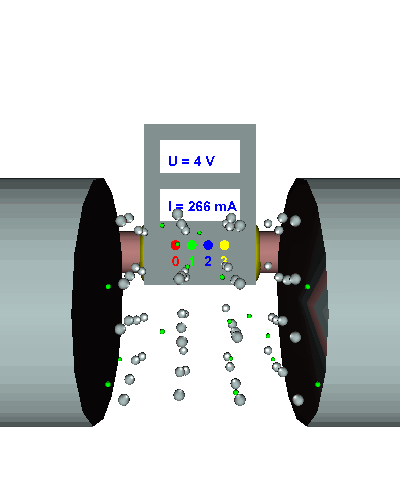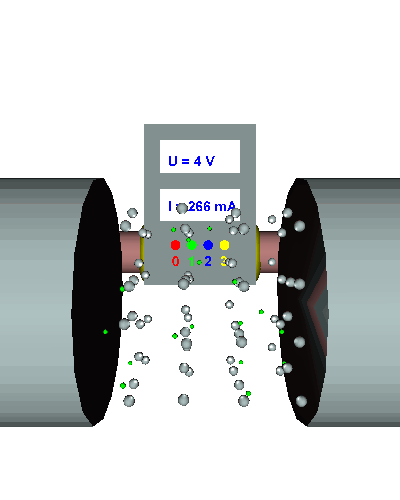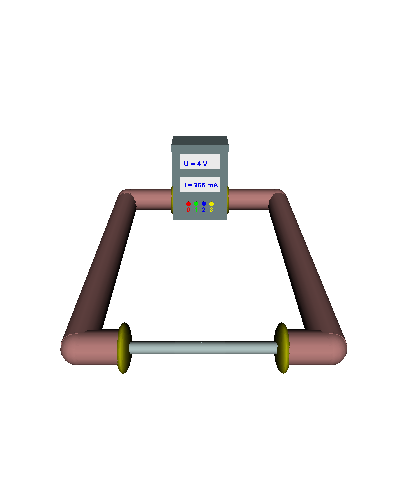
Einfacher Querschnitt

- Die gerichtet strömenden Elektronen werden durch den "Engpass" im Draht stark behindert ...

- die el. Stromstärke ist relativ gering ...

- der el. Widerstand folglich recht groß.

[ VRML-Animation ( 7 KB, Vollbild, interaktiv ) ]

Doppelter Querschnitt

- Die gerichtet strömenden Elektronen werden durch den doppelten "Engpass" nicht mehr ganz so stark behindert ...

- die el. Stromstärke nimmt zu ...

- der el. Widerstand wird kleiner.

[ VRML-Animation ( 9 KB, Vollbild, interaktiv ) ]

Dreifacher Querschnitt

- Die gerichtet strömenden Elektronen werden durch den dreifachen Querschnitt viel weniger behindert ...

- die el. Stromstärke nimmt weiter zu ...

- der el. Widerstand sinkt weiter.

Je größer der Querschnitt des el. Leiters, desto besser können sich die gerichtet strömenden Elektronen verteilen und werden um so weniger behindert. Es gilt:

 Der elektrische Widerstand R ist umgekehrt proportional zum Leiterquerschnitt A!
 

Da der el. Strom entsteht, wenn die Elektronen sich gerichtet durch den Leiter bewegen müssen sie natürlich an den Atomen und Ionen vorbei! Von diesen werden sie aber behindert - je länger nun der Draht ist, an um so mehr "Hindernissen" müssen sich die Elektronen also vorbeischlängeln. Daraus lässt sich logisch ableiten, dass der elektrische Widerstand mit zunehmender Länge ebenfalls zunimmt.

Schauen wir uns auch dazu eine entsprechende Versuchsreihe an:

[ VRML-Animation ( 5 KB, Vollbild, interaktiv ) ]

Einfache Länge

- Die gerichtet strömenden Elektronen     werden durch "einige" Hindernisse im Draht behindert ...

- die Elektronen werden nur relativ wenig behindert, die el. Stromstärke stellt sich auf einen konstanten Anfangswert in Abhängigkeit von der Spannung ein ...

- der el. Widerstand beträgt in diesem Beispiel R = 5 Ω!

[ VRML-Animation ( 5 KB, Vollbild, interaktiv ) ]

Doppelte Länge

- Mit der Länge des Leiters hat sich auch die Anzahl der Hindernisse im Draht verdoppelt ...

- die Elektronen werden doppelt so stark behindert, die el. Stromstärke sinkt auf die Hälfte des Anfangswerts ...

- der el. Widerstand verdoppelt sich dadurch und beträgt beträgt nun R = 10 Ω!

[ VRML-Animation ( 6 KB, Vollbild, interaktiv ) ]

Dreifache Länge

- Die gerichtet strömenden Elektronen werden nun noch mehr behindert ...

- die el. Stromstärke fällt auf ein Drittel ...

- der el. Widerstand erreicht den dreifachen Ursprungswert und beträgt damit nun 15 Ω.

 Der elektrische Widerstand R ist direkt proportional zur Länge l des Leiter!
 

 Herleitung des Widerstandsgesetztes

Der elektrische Widerstand verhält sich direkt proportional zur Länge des Leiters aber umgekehrt proportional zum Querschnitt des Leiters:

                 und                   

 Die mathematische Zusammenfassung beider Verhältnisse ergibt:

Um aus dieser Proportionalität eine Gleichung zu erhalten kommt nun noch das Material ins Spiel. Ein ein Meter langer Kupferdraht hat beispielsweise einen anderen Widerstand als ein gleichlanger Aluminiumdraht mit gleichem Querschnitt! Der Wert ρ (griechisch: rho) kennzeichnet den spezifischen elektrischen Widerstand eines Stoffes und gibt an, wie groß der elektrische Widerstand eines genormten Leiters (bezogen auf einen Meter Länge und einen Querschnitt von einem Quadratmillimeter) aus diesem Material  ist. Damit wird dem unterschiedlichen atomaren Aufbau verschiedener Leitermaterialien Rechnung getragen.

 Das Widerstandsgesetz

Der elektrische Widerstand R eines elektrischen Leiters kann nach folgender Formel berechnet werden:

Die Werte für ρ kann man Tabellen entnehmen. Dabei kann man sogar unterscheiden, welches Material zu den Leitern, den Isolatoren (Nichtleiter) oder den Halbleitern zählt:

Das war wieder eine ganze Menge Theorie! Also kommen nun zum Abschluss noch ein paar Übungen, um das Gelernte auch praktisch umzusetzen.

Viel Spaß bei den Übungen ;)

Übungen

1.) Umstellübungen

2.) formale Berechnungen

3.) Anwendungen

4.) Wheatstone'sche Brücke