|
Kapitel 7: Das Ohmsche Gesetz und der elektrische Widerstand |
|
|
Das Ohmsche Gesetz
beschreibt den Zusammenhang zwischen der elektrischen Spannung und der
elektrischen
Stromstärke. Nun macht es sich erforderlich, den Aufbau eines Metallgitters noch einmal genauer anzuschauen: |
|
|
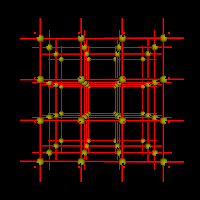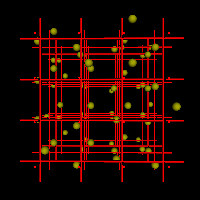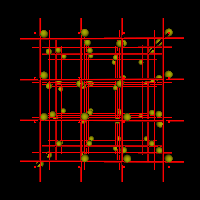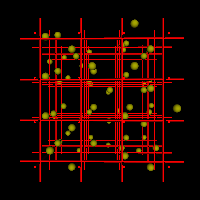
Das Metallgitter mit den Metallionen bzw. Metallatomen auf den Gitterplätzen. Im Idealfall sitzt auf jedem Gitterpunkt ein Atom oder Ion des Metalls. [ animiertes Gif ( 1 MB, 400 x ´400 ) ] [ VRML-Animation ( 3 KB, Vollbild, interaktiv ) ] |
In der Realität bewegen sich die Atome oder Ionen des Metalls auf Grund der Wärme. Man spricht von thermischen Schwingungen an den Gitterplätzen. [ animiertes Gif ( 0,6 MB, 400 x 400 ) ] [ VRML-Animation ( 3 KB, Vollbild, interaktiv ) ] |
|
Bei höherer Temperatur haben die Teilchen eine höhere Energie - sie schwingen heftiger und benötigen mehr Platz. [ animiertes Gif ( 0,5 MB, 400 x 400 ) ] [ VRML-Animation ( 3 KB, Vollbild, interaktiv ) ] |
Am heftigsten schwingen die Teilchen eines Metalls, wenn das Metall glüht! Das Material steht kurz vor dem Schmelzen. [ animiertes Gif ( 0,3 MB, 400 x 400 ) ] [ VRML-Animation ( 3 KB, Vollbild, interaktiv ) ] |
|
Was hat das nun aber mit dem Zusammenhang zwischen der elektrischen Spannung
und der elektrischen
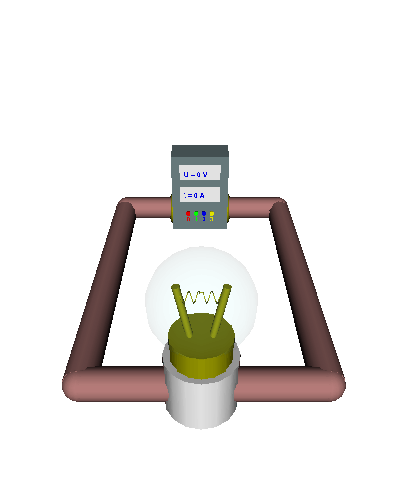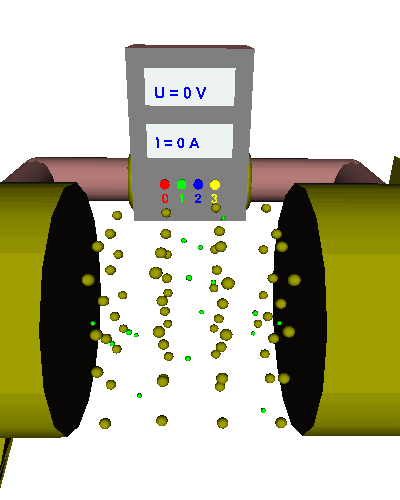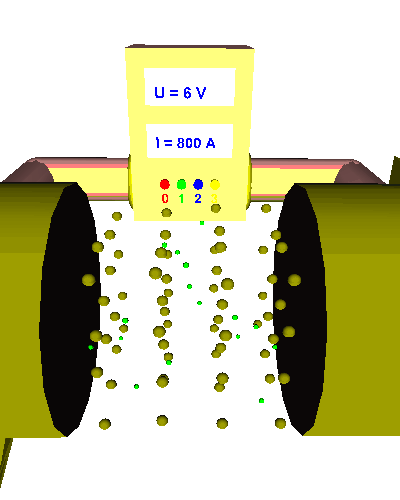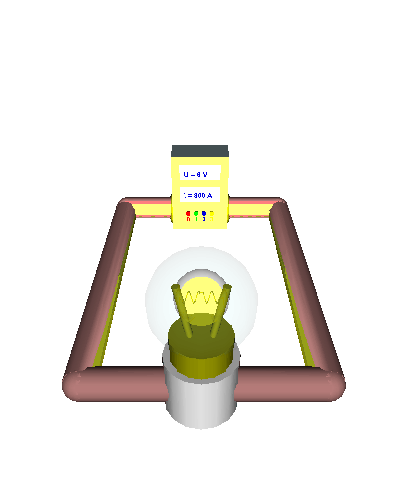
Stromstärke zu tun? Wir wissen ja bereits, dass el. Strom entsteht, wenn die Elektronen sich gerichtet durch den Leiter bewegen. Dazu müssen sie natürlich an den Atomen und Ionen - die ja an den Gitterplätzen schwingen - vorbei! Schauen wir uns das bei einem einfachen Drahtwiderstand an. Das Stromversorgungsgerät (oder auch die Spannungsquelle) ist gleichzeitig das Messgerät für die el. Spannung (U in V) und die el. Stromstärke (I in A). Braun dargestellt sind die Verbindungsleiter und der Widerstand aus Aluminiumdraht ist silbergrau dargestellt: |
|
|
[ animiertes Gif ( 2,7 MB, 400 x 500 ) ] [ VRML-Animation ( 8 KB, Vollbild, interaktiv ) ] [ DivX-Video ( 4,7 MB, 800 x 600 ) ] |
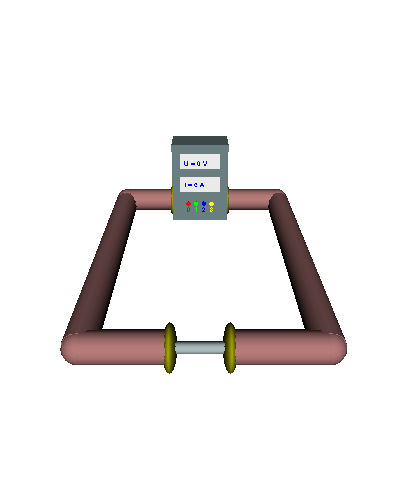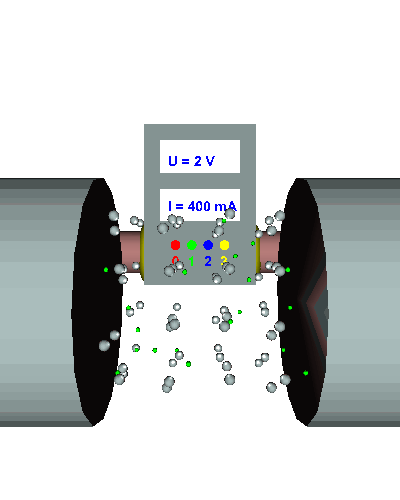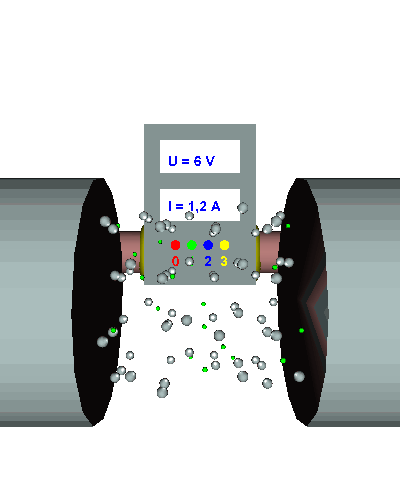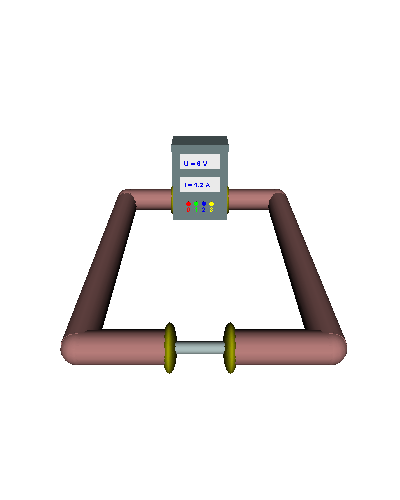
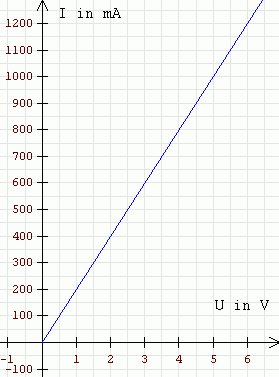
Bei Null Volt fließt gar keine el. Strom, da der
Antrieb der Elektronen ebenfalls Null ist. Bei zwei Volt Spannung ist ein geringer Stromfluss zu erkennen. Die el. Stromstärke beträgt 400 mA. Wenn wir die Spannung verdoppeln - also vier Volt wählen - dann verdoppelt sich auch die Zahl der Elektronen, die durch den Leiterquerschnitt fließen. Wir haben nun 800 mA Stromstärke. Zum Schluss wird die Spannung verdreifacht: Bei
nun 6 V beobachten wir eine el. Stromstärke von 1,2 A also Das Ergebnis ist nicht überraschend - genau damit haben wir gerechnet: Je größer der Antrieb des el. Stromes, desto größer ist auch die el. Stromstärke. Beachte jedoch, dass sich die Temperatur des Aluminiumdrahtes dabei nicht verändert hat. Das kann man an der gleich bleibenden Schwingung der Metallatome und Ione erkennen! |
| Im zweiten Beispiel schauen wir uns nun eine Glühlame als Widerstand an. Wenn wir die Lampe einschalten fängt die Glühwendel an zu glühen - die Lampe leuchtet. Jeder weiß, dass die Lampe - und also auch die Glühwendel - dabei heiß wird. Welchen Einfluss hat das auf die Stromstärke: | |
|
[ animiertes Gif ( 3 MB, 400 x 500 ) ] [ VRML-Animation ( 8 KB, Vollbild, interaktiv ) ] [ DivX-Video ( 5,5 MB, 800 x 600 ) ]
|
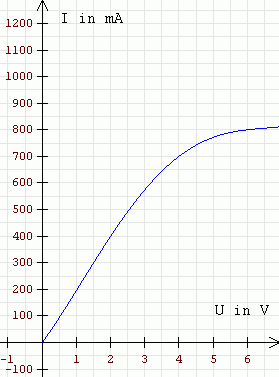
Bei Null Volt fließt gar keine el. Strom, da der
Antrieb der Elektronen ebenfalls Null ist. Bei zwei Volt Spannung ist ein geringer Stromfluss zu erkennen. Die el. Stromstärke beträgt 400 mA. Wenn wir die Spannung verdoppeln - also vier Volt wählen - dann erwarten wir auch eine Verdoppelung der Stromstärke - aber wir erhalten anstatt der erwarteten 800 mA nur 700 mA also deutlich weniger ... Zum Schluss wird die Spannung verdreifacht: Bei nun 6 V beobachten wir eine el. Stromstärke von 800 mA also viel weniger als das Dreifache der Ausgangsstromstärke!!! Auch dieses Ergebnis ist jedoch nicht überraschend, wenn man bedenkt, dass sich die Temperatur der Glühwendel dabei stark erhöht hat. Die thermischen Schwingungen der Metallatome und Ione sind deutlich hektischer geworden! Dadurch stoßen sie viel häufiger mit den hindurcheilenden Elektronen zusammen und bremsen diese ab => der el. Widerstand des Leiters erhöht sich durch die Temperaturerhöhung!!! |
|
Zusammenfassung: Ohmsches Gesetz Die elektrische Stromstärke I in einem Bauelement ist der angelegten elektrischen Spannung U direkt proportional, solange sich die Temperatur des Leiters nicht verändert! |
|