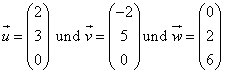
| Das Spatprodukt letztendlich ist eine Zusammensetzung aus dem Kreuzprodukt und dem Skalarprodukt. Um ein Spatprodukt berechnen zu können, benötigt man drei Ausgangsvektoren. Die ersten zwei Vektoren werden kreuzmultipliziert und das Ergebnis anschliessend mit dem dritten Vektor skalarmultipliziert. Gehen wir also von folgenden drei Vektoren aus: |
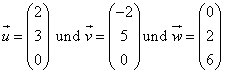
| Diese Vektoren werden nun, wie oben beschrieben, miteinander verknüpft: |
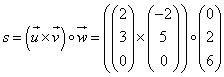
| Jetzt führen wir zuerst die Kreuzmultiplikation aus: |
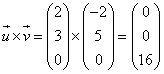
| Und danach kommt die Skalarmultiplikation dieses Zwischenergebnisses mit dem Vektor w: |
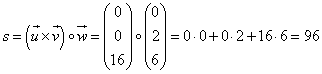
| Das Ergebnis des Spatproduktes ist also 96! Aber was hat es mit dieser
Zahl nun auf sich?
Offensichtlich handelt es sich hierbei um eine skalare Größe. Ausserdem heißt diese Rechenoperation "Spatprodukt"! Also muß ein direkter Zusammenhang zwischen dem Ergebnis und dem Spat bestehen. Ein Spat ( Fachbegiff: Parallelepiped ) ist ein geometrischer Körper mit einem bestimmten Volumen. Und genau dieses Volumen berechnen wir mit dem Spatprodukt! |
| Die 3D-Grafik zeigt die Lage des Parallelepipedes beim Spatprodukt von Vektoren. |
|
|
Zuerst sieht man die drei ursprünglichen Vektoren (u-rot, v-blau, w-grün). Nun kann man die Hilfslinien zu den Vektoren einblenden. Dann wird der Parallelepiped (gelb) angezeigt. Das Spatprodukt beschreibt das Volumen dieses Parallelepipedes! |
|
| In diesem Beispiel wurde die Lage der ersten beiden Vektoren so gewählt, daß sie beide in der x-y-Ebene liegen. Das erleichtert uns die Anschaulichkeit des Parallelepipedes. |