|
Das Vervielfachen eines Vektors Wenn ein Vektor mit einer reellen Zahl multipliziert wird, dann müssen alle drei Koordinaten des Vektors mit dieser Zahl multipliziert werden. 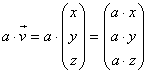 Unter Verwendung von Zahlen sieht das dann so aus:
|
|
Man unterscheidet drei verschiedene Arten, wie man Vektoren multiplizieren kann:
|
|
Das Vervielfachen eines Vektors Wenn ein Vektor mit einer reellen Zahl multipliziert wird, dann müssen alle drei Koordinaten des Vektors mit dieser Zahl multipliziert werden. 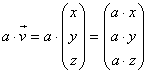 Unter Verwendung von Zahlen sieht das dann so aus:
|
|
Der dunkelblaue Vektor soll um den Faktor 2,5 gestreckt werden. |
|
|
|
Das Skalarprodukt von zwei Vektoren Die zweite Möglichkeit, Vektoren zu multiplizieren, ist das Skalarprodukt. Wie Name schon sagt ist das Ergebnis in diesem Fall ein Skalar und kein Vektor. Trotzdem hat das Skalarprodukt seine Berechtigung, denn das Ergebnis weist eine Besonderheit auf, die das Skalarprodukt interessant macht. Allgemein berechnen wir das Skalarprodukt indem wir die Koordinaten der Vektoren paarweise multiplizieren und die Produkte addieren:
Beachte, daß diese Multiplikation nicht durch einen Punkt sondern durch einen kleinen Kreis symbolisiert wird! Sehen wir uns nun zwei Beispiele mit konkreten Zahlenwerten an:
Was ist nun aber das Besondere an den Ergebnissen? Schauen wir uns als drittes Beispiel zwei Vektoren an, die senkrecht aufeinander stehen: 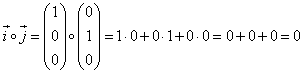 Wir sehen sofort, daß das Skalarprodukt Null ist - genau wie der Kosinus des Winkels von 90°!!! Genauere Untersuchungen zeigen dann auch folgenden Zusammenhang:
Für das obere Beispiel erhalten wir somit: 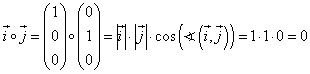 Diese Erkenntnis erlaubt es uns nun den Winkel, den zwei Vektoren einschließen, zu bestimmen! Dazu stellen wir den oberen allgemeinen Zusammenhang nach dem Kosinus des Winkels um:
|
|
Die beiden Ortsvektoren werden skalar multipliziert. Mit dem Skalarprodukt und den Beträgen der Vektoren kann der - von den Vektoren eingeschlossene - Winkel berechnet werden. |