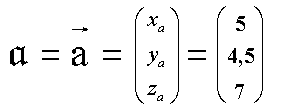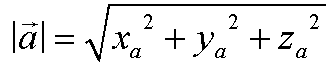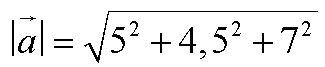|
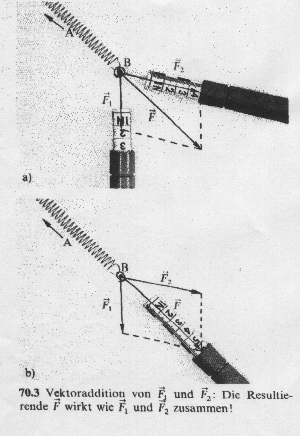
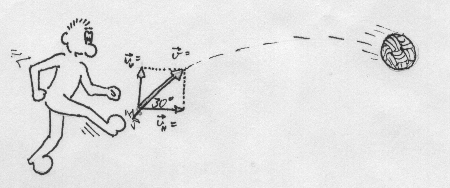
Der Begriff Vektor ist ja bereits aus dem Physikunterricht bekannt - Zur Erinnerung: Kräfte, Geschwindigkeiten oder Beschleunigungen waren vektorielle Größen, da sie nur durch die Angabe von Betrag, Richtung und Anfangspunkt genau beschrieben werden konnten (Skizzen). Andere Größen, wie z. B. die Masse oder die Temperatur, sind skalare Größen. Das bedeutet, daß die Angabe des Betrages (natürlich immer mit der entsprechenden Einheit!) ausreicht, um sie genau zu beschreiben. In der Mathematik ist der Vektor vom Prinzip her das Gleiche wie in der Physik. Größen, die durch die Angabe von Betrag, Richtung und Anfangspunkt bestimmt werden müssen, sind Vektoren. Zur Kennzeichnung verwenden wir Pfeile: Länge des Pfeils - Betrag des Vektors,
Das sieht in verschiedenen Mathematikprogrammen dann so aus:
Um einen Vektor sofort von einer anderen Größe unterscheiden zu können verwendet man zur Bezeichnung entweder altdeutsch Buchstaben oder Buchstaben mit einem Pfeil darüber: 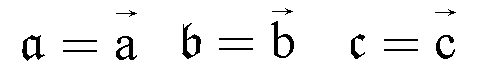 Wenn Vektoren im dreidimensionalen Raum liegen, werden sie durch drei Koordinatenangaben gekennzeichnet. Jeder Vektor hat eine x-Koordinate, eine y- Koordinate und eine z-Koordinate. Diese werden durch Klammern zusammengefaßt, aber (anders als bei Punkten) nicht nebeneinander sondern übereinander. Das sieht dann z. B. so aus:
|
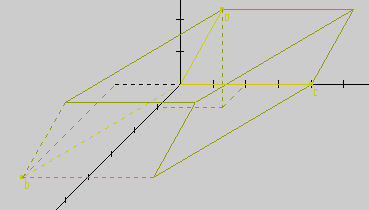
| Im Beispiel ist der Vektor hellblau dargestellt. Wenn man auf START
klickt werden die Koordinaten angezeigt. Zur besseren Veranschaulichung
sind diese als Seiten eines Quaders dargestellt, der den Vektor als Raumdiagonale
hat! Das Koordinatensystem ist frei beweglich, d.h. mit Hilfe der Konsole
darunter kann man das System rotieren lassen, zoomen und ähnliches
mehr, um sich einen räumlichen Eindruck davon zu verschaffen: |
|
|
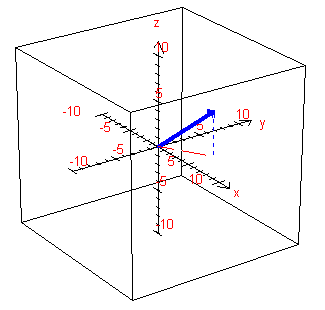
Hier sieht man einen Vektor (schwarz). Da dieser Vektor im Koordinaten-Ursprung beginnt nennt man ihn Ortsvektor. Das bedeutet, er weist die Richtung vom Koordinaten-Ursprung zu einem Ort im Raum (KOS)! Um die Lage des Vektors im Raum besser erkennen zu können legt man einen Quader mit den entsprechenden Abmessungen mit in den Raum. Wenn man nun nur noch die Kanten des Quaders anzeigen lässt, die den Koordinaten entsprechen, dann ergibt sich ein klares Bild der Lage des Vektors im Raum. |
|