Ortsvektoren und Repräsentanten

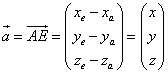
Grundsätzlich werden in der Vektorgeometrie zwei Arten von Vektoren unterschieden: Ortsvektoren und Repräsentanten!
Vektoren werden als Ortsvektoren bezeichnet, wenn ihre Anfangspunkte mit dem Koordinatenursprung übereinstimmen.
Das heißt, Ortsvektoren zeigen immer vom Punkt (0;0;0) auf einen Punkt im Raum!
Repräsentanten von Ortsvektoren können jedoch beliebig im Raum liegen. Ein Vektor ist also die unendliche (warum???) Menge aller Repräsentanten, die den selben Ortsvektor darstellen!

Um nun von beliebigen Vektoren (die durch Anfangs- und Endpunkt gegeben sind) den Ortsvektor zu bestimmen, den sie repräsentieren, muß man die Differenz der Koordinaten bilden. Man subtrahiert von den Koordinaten des Endpunktes die Koordinaten des Anfangspunktes:

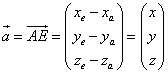
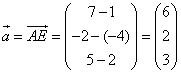
Im konkreten Fall sieht das dann so aus: Ein Vektor der vom Anfangspunkt A (1,-4,2) zum Endpunkt E (7,-2,5) verläuft, der repräsentiert den Ortsvektor vom Koordinatenursprung (0,0,0) zum Punkt (6,2,3).


Im Beispiel ist der Ortsvektor hellblau dargestellt. Wenn man auf START klickt werden einige Repräsentanten erzeugt. Diese Repräsentanten (hellbraun dargestellt) haben die selbe Richtung und den selben Betrag wie der Ortsvektor, aber ihr Anfangspunkt ist beliebig.

Wenn du nun noch ein paar Übungen selbst rechnen möchtest, dann klicke jetzt die
Übungsseite zu Ortsvektoren und Repräsentanten an!

[ Übungen ]   [ zurück zur Übersicht ]   [ Vektoraddition ]