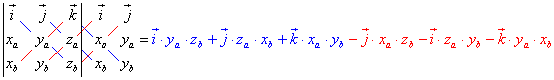Anwendung zur Vektorrechnung
Ein Problem welches sich häufig stellt, ist die Berechnung von Flächeninhalten im Raum:
| Aufgabe: Gegeben seien drei Punkte im Raum. Gesucht ist die Fläche
des Dreiecks, das durch
diese Punkte gebildet wird! geg.: P1 = ( 4, 5, 2)
ges.: Fläche des Dreiecks
1. Lösungsschritt: Wir betrachten dazu an Stelle der Punkte drei Vektoren (Ortsvektoren)! 2. Lösungsschritt: Anhand der Ortsvektoren bestimmen
wir zuerst zwei Richtungsvektoren, die
3. Lösungsschritt: Der Betrag des Kreuzproduktes
der Richtungsvektoren ist flächengleich zu
Als Formel sieht das dann so aus:
|
Die graphische Veranschaulichung soll dir helfen, das Prinzip besser zu verstehen:
| Auf einer Ebene im Raum befinden sich drei Punkte. Mit der Maus kann die Lage dieser Punkte verändert werden! Es bildet sich ein Dreieck, dessen Flächeninhalt zusammen mit den Punktkoordinaten angezeigt wird: |
|
Punkt 2
|
- |
Punkt 1
|
= |
Richtungsvektor
|
|
Punkt 3
|
- |
Punkt 1
|
= |
Richtungsvektor
|
|
|
|
=
*
*
+
*
*
+
*
*
-*
*
-*
*
-*
*
=
*+
*+ *
|
|
|
|
|
