|
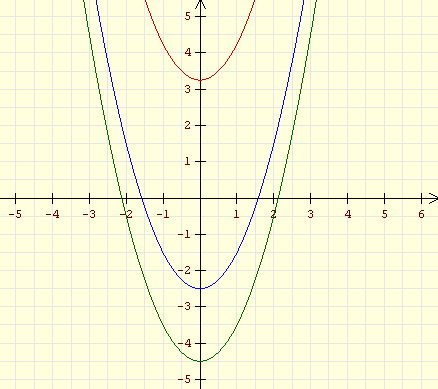
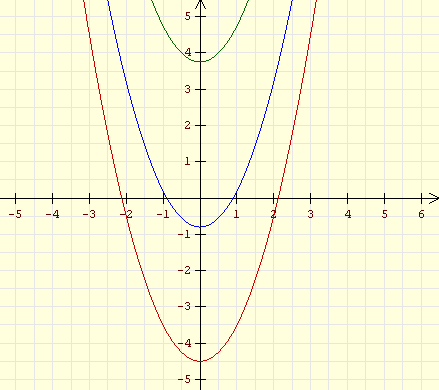
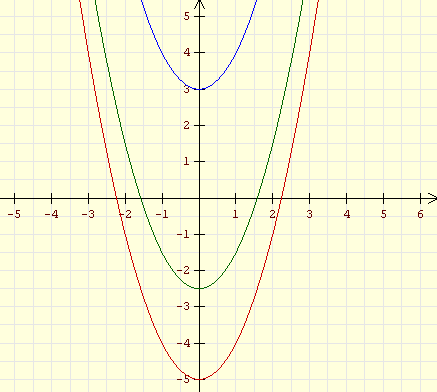
(vertikal verschobene Normalparabeln) |
|
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
|
||||||||||||||||
|
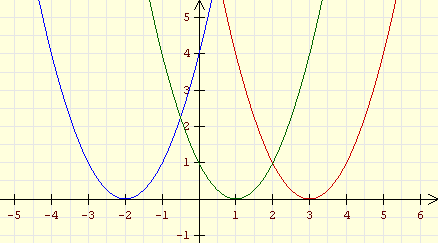
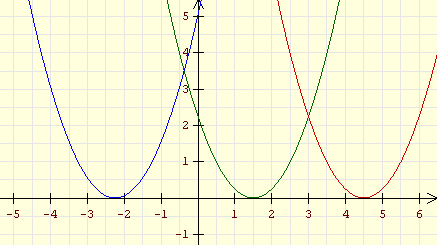
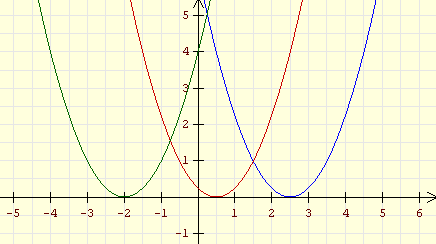
(horizontal verschobene Normalparabeln) |
|
||||||||||||||||
 |
aaaa
|
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
|
||||||||||||||||
|
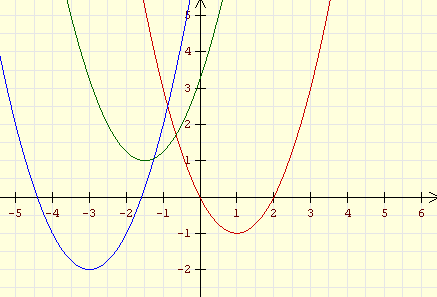
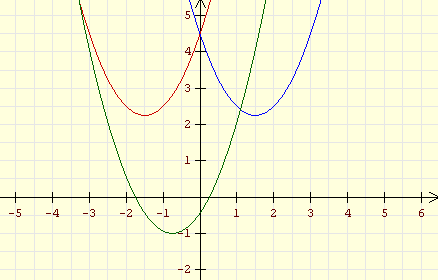
(verschobene Normalparabeln) |
|
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
|
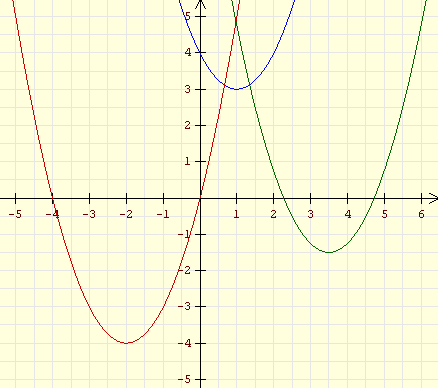
Alle Aufgaben dieser Seite beziehen sich auf Funktionen
mit den Funktionsgleichungen
y = x2 +b ,
y
= (x + d)2 oder y = (x + d)2
+b
also auf verschobene Normalparabeln!
Wenn du Hilfe brauchst verwende den Funktionsgraphen-Plotter
um verschiedene Funktionen der Form
y = ( x + d )^2 + b zu zeichnen und dann die unten abgebildeten
Graphen darzustellen!
|
(vertikal verschobene Normalparabeln) |
|
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
|
||||||||||||||||
|
(horizontal verschobene Normalparabeln) |
|
||||||||||||||||
 |
aaaa
|
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
|
||||||||||||||||
|
(verschobene Normalparabeln) |
|
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
aaaa |
||||||||||||||||
 |
|