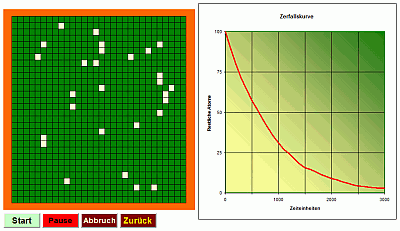
Radioaktive Halbwertszeit

Die Halbwertszeit ist in der Kernphysik diejenige Zeitspanne, in der die Menge eines bestimmten radioaktiven Nuklids auf die Hälfte gesunken ist, das heißt sich in andere Atome umgewandelt hat. Für jedes Nuklid ist die Halbwertszeit eine Konstante.

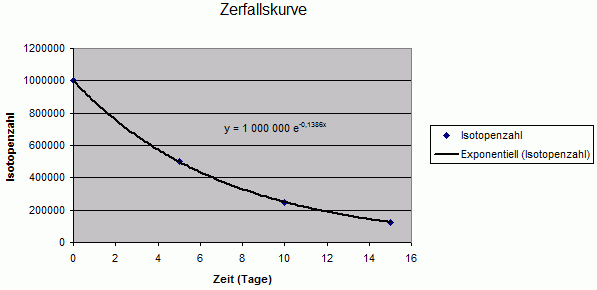
Sehr schön beobachten lässt sich dies anhand der Excel-Tabelle von von Berthold Gabel:

[ Excel-Tabelle öffnen ]

Die Anzahl der verbleibenden Kerne zu einer bestimmten Zeit ist durch eine exponentielle Zerfallskurve zu bestimmen. Das ist eine Kurve, die bei einem bestimmten Startwert auf der y-Achse (Isotopenzahl) beginnt und dann erst steil abfällt - aber mit der Zeit immer flacher verläuft ohne die x-Achse (Zeit) jemals zu berühren. Rein mathematisch betrachtet verschwindet die radioaktive Substanz also nie, physikalisch ist natürlich mit der Umwandlung des letzten Atoms eine Grenze gesetzt (die Substanz komplett verschwunden).

Beispiel: Halbwertzeit T_1/2=5 Tage

Wie man deutlich erkennt halbiert sich die Anzahl der radioaktiven Isotope alle 5 Tage.

Beispiel: Halbwertzeit T_1/2=3 Tage

[ Übung im Diagramm ]